Basic FEM

Table of contents

Video lectures

Variational Formulation - The weak form

We cannot directly tackle the strong form of a differential equation to create the FEM. The first step in the FEM is to derive the weak form (or variational form) of the strong form.

Consider the model problem

From the strong form we can formulate the residual function

This strong form must hold everywhere for $x\in[0,L]$. Now, the central idea of the weak form is to turn this point-wise residual into an average, following the approach by Liu in [2], we start by creating an integral equation

here, we integrate the residual over the entire domain and set it to zero, we are basically saying that, on average, the residual should be zero. This essentially turns the strong form of the residual into a weak form, and given that we naively integrate it over the entire domain, we seem to have the equation hold "too weak". We could instead integrate (average) over a smaller region around some arbitrary point $x$

thus we can control how far away from the point-wise zero point we are by varying $\Delta x$. This idea can be extended to all locations in the domain $x\in[0,L]$ and we end up with a set of integral equations that approximate the strong form of the differential equation

where we have split the original domain into $N$ subdomains and thus we end up with a set of $N$ integral equations. The more subdomains we use, the better our approximation and in the limit we have that with $N\rightarrow\infty$ we get $\int_{x_{1}}^{x_{2}}r(x)dx\rightarrow r(x)$.

Now, stating the weak form as a set of arbitrarily many integral functions is cumbersome and limits its potential, we can instead multiply the residual with a function, $v$ that is non-zero only in a narrow range. This function is known as the test function (a.k.a. weight function) and is arbitrary, meaning that it actually is a set of functions, in fact infinitely many. Another requirement on the test function is that it needs to be zero at the boundary where the solution is known, e.g., for our example above $v(0) = 0$. The solution $u(x)$ is really also a member of the same set of functions as the test function. Therefore the solution is also known as the trial function.

We can now integrate the product $r(x)v(x)$ over the entire domain $[0,L]$ for a variety of functions $v(x)$. The test functions limit the contribution of the residual to their respective subdomain and we achieve a similar effect as the set of integral equations above, see Figure 1 for an illustration of the concept.

In the above, $\forall v:v=0$ reads: for all $v$ such that $v$ is zero at $x=0$. This means that the integral has to hold for all arbitrary functions $v$ and that the test functions need to be constructed such that they all are 0 on the border where the solution, $u$ is known to ensure that boundary condition.

We end up with

but what about the boundary conditions for the original model problem in (1)? Also, we have not really made things simpler with our integral equation, it still contains a second order derivative. We shall address both issues now with integration by parts.

Finally we add this to our integral from above

and we end up with the weak form of our model problem

If we expand the last term we get

note that $k\dfrac{du}{dx}(L)=-q$ and that $v(0)=0$ since $u$ is known at $x=0$, this is why we construct the test function in such a way.

We shall soon see that when solving the weak form, we seek a set of admissible solutions $u(x)$ (a.k.a. trial solutions or trial functions).

We could have skipped the integration by parts and used the original weak form to create the finite element method but our test function would require to be two times differentiable, not a big issues in it self. Also, the resulting matrix system would not be symmetric, which is nice to have for the sake of performance. Furthermore, the boundary conditions would need special treatment.

The recipe for getting to the weak form

Minimum of potential energy

The model problem can also be formulated as a minimization problem: find $u$ such that $F(u)\leq F(v)$ for all admissable functions $v$, where

The functional $F$ represents the potential energy of the physical system obeying the model problem, and thus the actual solution to our physical problem is the one that minimizes potential energy.

More on the weak formulation

There exist several alternative numerical methods for solving differential equations, e.g., the Finite Difference Method which is a more direct approach for solving differential equations. The reader might ask, why not just approximate the differential directly using e.g.,

which is indeed straight forward and will lead to a linear system of equations which is sparse, symmetric and efficient to implement and solve. The problem is that it is troublesome to use it in several dimensions for problems with even just a fairly complicated geometry. Arguably the FEM is more general and robust but not as straight forward and easy to implement.

The strength of the weak form

For some problems there exists a principle of minimum potential energy which leads to the weak form. These approaches usually are physics based and give a physical meaning to the test function, e.g., in mechanics the test functions are "virtual displacements" and the problem of finding the weak form is treated as a minimization of potential energy. It can be argued that the mathematical approach of multiplying the strong form by a test function and integrating by parts is more general since there might not exists a principle of minimum potential energy.

Not all physical problems can be idealized by simple models and sometimes discontinuities emerge in the models, either by the models them selves or by parameters of the models (material parameters in particular). These non-smooth functions cause the derivatives to be ill-defined, thus the strong form of the differential equation fails to describe the physics in each point and the integral formulation of the weak form better describes the physics on average.

Alex from Beyond the Big Bang YouTube channel did an outstanding introduction of the differential equation

and deriving the weak formulation.

A more detailed example of the strength of the weak form can be found in Section 4.4.1 in [1] where a 1D example is derived handling a discontinuous material parameter.

Examples

Example 1

Consider the residual function

$$r(x)=x+\dfrac{\sin(7x)}{2}+3\ \text{for }x\in[0,1]$$

if we split the domain into $N=4$ equal subdomains and choose the test-function to be a linear function then for the second subdomain (or element), $x \in [0.25\ 0.5]$, the test functions look like this

3: A test function for element 2

So every element is essentially made up of a set of functions, in this example, two, that multiply the residual function. If we take the sum of this product

$$\sum_{i=1}^{n}r(x)v_{i}(x)=r(x)$$

in our example $n=2$, we see that for any $x$ if we multiply the test functions from one element with our residual function and take the sum then we get back the residual function! We will study this property in more details in upcoming sections.

Here is a animation to showcase this effect

4: The set of test functions for four elements.

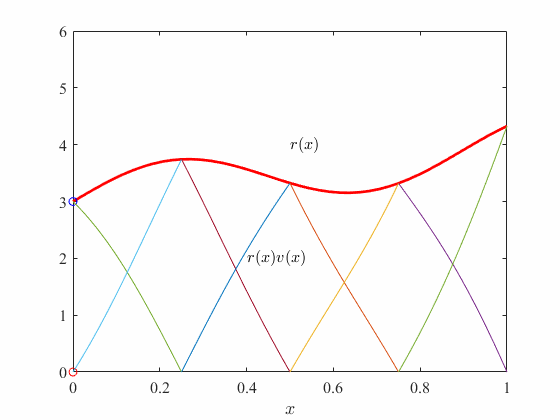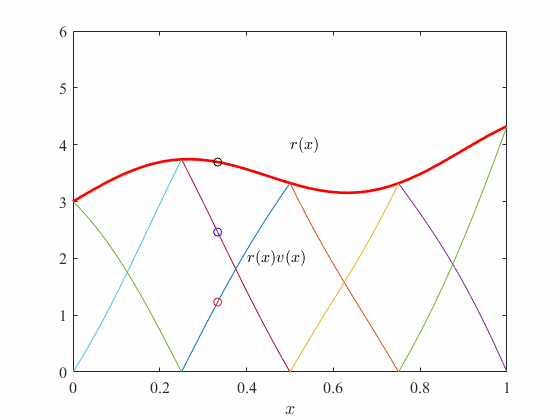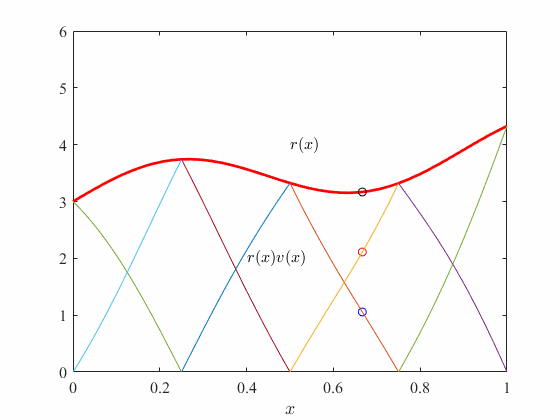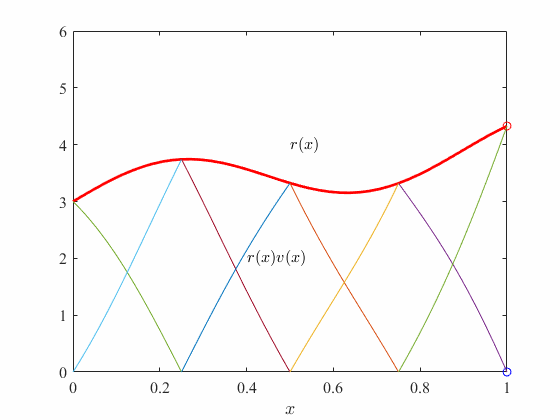
In the above, every subdomain (element) has a set of test functions (in this case two), for which the linear combination yields the residual, or

$$\sum_{i=1}^2 r(x)\varphi_i(x) = r(x)$$

where $\varphi_i(x)$ is known as the basis function when it is applied concretly on an element.

References