Basic FEM

by Mirza Cenanovic & Carl-Johan Jonsson

Table of contents

  1. Computing stress from displacements
  2. Example 1 - A simple rectangle
  3. Example 2 - Linear triangles
  4. Example 3 - Quadrilateral
  5. Nodal averaging - L2L_2 projection
  6. Example 4 - Nodal averaging a triangular mesh
    1. Verification of the model
    2. Computing the stress
  7. References

Computing stress from displacements

The stress matrix is given by

σ=2με+λtrεI\bm \sigma =2\mu \bm \varepsilon +\lambda \mathrm{tr} \bm \varepsilon \bm I

Computing the strain

ε=[∂ux  ∂x12(∂ux  ∂y+∂uy  ∂x)12(∂ux  ∂y+∂uy  ∂x)∂uy∂y]=12(∇uT+∇u) \def\arraystretch{2.5} \bm \varepsilon =\left\lbrack \begin{array}{cc} \dfrac{\partial u_x \;}{\partial x} & \dfrac{1}{2}\left(\dfrac{\partial u_x \;}{\partial y}+\dfrac{\partial u_y \;}{\partial x}\right)\\ \dfrac{1}{2}\left(\dfrac{\partial u_x \;}{\partial y}+\dfrac{\partial u_y \;}{\partial x}\right) & \dfrac{\partial u_y }{\partial y} \end{array}\right\rbrack =\dfrac{1}{2}\left(\nabla \bm u^T +\nabla \bm u\right) ∇u=[∂ux  ∂x∂uy  ∂x∂ux  ∂y∂uy  ∂y] \def\arraystretch{2.5} \nabla \bm u=\left\lbrack \begin{array}{cc} \dfrac{\partial u_x \;}{\partial x} & \dfrac{\partial u_y \;}{\partial x}\\ \dfrac{\partial u_x \;}{\partial y} & \dfrac{\partial u_y \;}{\partial y} \end{array}\right\rbrack ∂ux  ∂x≈∑  ∂φi∂xux,i=∂φ∂x⋅Ux\dfrac{\partial u_x \;}{\partial x}\approx \sum_{\;} \dfrac{\partial \varphi_i }{\partial x}u_{x,i} =\dfrac{\partial \bm \varphi }{\partial x}\cdot {\mathbf{U} }_x ∂φ∂x=B=[∂φ∂x∂φ∂y]=[∂φ1∂x∂φ2∂x∂φ3∂x⋯∂φ1∂y∂φ2∂y∂φ3∂y⋯] \def\arraystretch{2.5} \dfrac{\partial \bm \varphi }{\partial x}=\mathbf{B}=\left\lbrack \begin{array}{c} \dfrac{\partial \bm \varphi }{\partial x}\\ \dfrac{\partial \bm \varphi }{\partial y} \end{array}\right\rbrack =\left\lbrack \begin{array}{cccc} \dfrac{\partial \varphi_1 }{\partial x} & \dfrac{\partial \varphi_2 }{\partial x} & \dfrac{\partial \varphi_3 }{\partial x} & \cdots \\ \dfrac{\partial \varphi_1 }{\partial y} & \dfrac{\partial \varphi_2 }{\partial y} & \dfrac{\partial \varphi_3 }{\partial y} & \cdots \end{array}\right\rbrack U=[u1xu1yu3xu2yu3xu3y⋮⋮] \def\arraystretch{1.5} \mathbf{U}=\left\lbrack \begin{array}{cc} u_1^x & u_1^y \\ u_3^x & u_2^y \\ u_3^x & u_3^y \\ \vdots & \vdots \end{array}\right\rbrack ∇U=[∂Ux  ∂x∂Uy  ∂x∂Ux  ∂y∂Uy  ∂y]=B  U \def\arraystretch{2.5} \nabla \mathbf{U}=\left\lbrack \begin{array}{cc} \dfrac{\partial U_x \;}{\partial x} & \dfrac{\partial U_y \;}{\partial x}\\ \dfrac{\partial U_x \;}{\partial y} & \dfrac{\partial U_y \;}{\partial y} \end{array}\right\rbrack =\mathbf{B}\;\mathbf{U} B=J−1B^  \mathbf{B}=\bm J^{-1} \hat{\mathbf{B} } \; J=B^  P\bm J =\hat{\mathbf{B} } \;\mathbf{P} B^=[∂φ^∂ξ∂φ^∂η]=[∂φ1∂ξ∂φ2∂ξ∂φ3∂ξ⋯∂φ1∂η∂φ2∂η∂φ3∂η⋯]=lin.tri.[−110−101] \def\arraystretch{2.5} \hat{\mathbf{B} } =\left\lbrack \begin{array}{c} \dfrac{\partial \hat{\varphi } }{\partial \xi }\\ \dfrac{\partial \hat{\varphi } }{\partial \eta } \end{array}\right\rbrack =\left\lbrack \begin{array}{cccc} \dfrac{\partial \varphi_1 }{\partial \xi } & \dfrac{\partial \varphi_2 }{\partial \xi } & \dfrac{\partial \varphi_3 }{\partial \xi } & \cdots \\ \dfrac{\partial \varphi_1 }{\partial \eta } & \dfrac{\partial \varphi_2 }{\partial \eta } & \dfrac{\partial \varphi_3 }{\partial \eta } & \cdots \end{array}\right\rbrack \overset{\textrm{lin}\ldotp \textrm{tri}\ldotp }{=} \left\lbrack \begin{array}{ccc} -1 & 1 & 0\\ -1 & 0 & 1 \end{array}\right\rbrack P=[p1xp1yp2xp2yp3xp3y⋮⋮]\mathbf{P}=\left\lbrack \begin{array}{cc} p_1^x & p_1^y \\ p_2^x & p_2^y \\ p_3^x & p_3^y \\ \vdots & \vdots \end{array}\right\rbrack

Example 1 - A simple rectangle

We construct a rectangle under pure tension, meaning we only expect stress in the x-direction.

Material data

E = 2200; %MPa
nu = 0.33;

%Plane Stress
lambda = E*nu/(1-nu^2);
mu = E/(2*(1+nu));

P = [0,0
     3,0
     3,1
     0,1];
U = [0 0
     1 0
     1 0
     0 0]/100;
L = (P(2,1)-P(1,1));
εx=deformationoriginal  length=1/1003\varepsilon_x =\dfrac{\textrm{deformation} }{\textrm{original}\;\textrm{length} }=\dfrac{1/100}{3} 
epsx = U(2,1) / L;
εy=−νεx\varepsilon_y ={-\nu \varepsilon }_x 
epsy = -nu * epsx;
uy=εyhu_y =\varepsilon_y h 
U(3:4,2) = epsy*1;
figure
patch(P(:,1),P(:,2),'w')
axis equal tight off; hold on
patch(P(:,1)+U(:,1)*20,P(:,2)+U(:,2)*20,'w','LineStyle',':', ...
    'FaceColor','none')

Compute the stress matrix, von Mises stress and principal stresses for the element. Let E=2200MPaE=2200\textrm{MPa}, ν=0.33\nu =0\ldotp 33. Use plane stress.

Basis functions

phi = @(xi,eta)[(eta-1.0).*(xi-1.0),-xi.*(eta-1.0),eta.*xi,-eta.*(xi-1.0)];
Bh = @(xi,eta)[eta-1, 1-eta, eta, -eta;
               xi-1,  -xi,   xi,  1-xi ];

We shall evaluate the stress in the midpoint.

xi = 0.5; eta = 0.5;
B=J−1B^  \mathbf{B}={\mathbf{J} }^{-1} \hat{\mathbf{B} } \; J=B^  P\bm J =\hat{\mathbf{B} } \;\mathbf{P} 
J = Bh(xi,eta)*P;
B = J\Bh(xi,eta);

Gradient of uu

∇u≈∇U=[∂Ux  ∂x∂Uy  ∂x∂Ux  ∂y∂Uy  ∂y]=B  U \def\arraystretch{2.5} \nabla \bm u\approx \nabla \mathbf{U}=\left\lbrack \begin{array}{cc} \dfrac{\partial U_x \;}{\partial x} & \dfrac{\partial U_y \;}{\partial x}\\ \dfrac{\partial U_x \;}{\partial y} & \dfrac{\partial U_y \;}{\partial y} \end{array}\right\rbrack =\mathbf{B}\;\mathbf{U} 
gradU = B*U;
ε=[∂ux  ∂x12(∂ux  ∂y+∂uy  ∂x)12(∂ux  ∂y+∂uy  ∂x)∂uy∂y]=12(∇uT+∇u) \def\arraystretch{2.5} \bm \varepsilon =\left\lbrack \begin{array}{cc} \dfrac{\partial u_x \;}{\partial x} & \dfrac{1}{2}\left(\dfrac{\partial u_x \;}{\partial y}+\dfrac{\partial u_y \;}{\partial x}\right)\\ \dfrac{1}{2}\left(\dfrac{\partial u_x \;}{\partial y}+\dfrac{\partial u_y \;}{\partial x}\right) & \dfrac{\partial u_y }{\partial y} \end{array}\right\rbrack =\dfrac{1}{2}\left(\nabla \bm u^T +\nabla \bm u\right) 
epsilon = 1/2*(gradU'+gradU)
epsilon = 2x2    
    0.0033         0
         0   -0.0011
sigma = 2*mu*epsilon + lambda*trace(epsilon)*eye(2)
sigma = 2x2    
    7.3333         0
         0   -0.0000

Principal stress

[V,D] = eig(sigma);
sigmaPrinc = diag(D);
dir = V;
dir = 2x2    
     1     0
     0     1
sigmaPrinc = sigmaPrinc(ind)
sigmaPrinc = 2x1    
    7.3333
   -0.0000
xm = mean(P,1);
hold on; scale = 0.3;
quiver(xm(1),xm(2),dir(1,1),dir(2,1),scale,'b','Displayname','1st principal direction')
quiver(xm(1),xm(2),-dir(1,1),-dir(2,1),scale,'b','HandleVisibility','off')
quiver(xm(1),xm(2),dir(1,2),dir(2,2),scale,'r','Displayname','2nd principal direction')
quiver(xm(1),xm(2),-dir(1,2),-dir(2,2),scale,'r','HandleVisibility','off')

sigma_vm = sqrt(sigma(1,1)^2-sigma(1,1)*sigma(2,2)+sigma(2,2)^2+3*sigma(1,2)^2)
sigma_vm = 7.3333

annotation(gcf,'textbox',...
    [0.030 0.818 0.3 0.14],...
    'String', ...
    {['$\theta=$',sprintf(' %0.0f',theta),'$^\circ$'], ...
    ['$\sigma_1=$',sprintf(' %0.2f',sigmaPrinc(1)),'MPa'], ...
    ['$\sigma_2=$',sprintf(' %0.2f',abs(sigmaPrinc(2))),'MPa'], ...
    ['$\sigma_{vM}=$',sprintf(' %0.2f',sigma_vm),'MPa']}, ...
    'LineStyle','none', ...
    'Interpreter','latex', ...
    'FitBoxToText','off');

annotation(gcf,'textbox',...
    [0.7 0.13 0.130357139504382 0.145238091619242],...
    'String', ...
    {['$\sigma =\left\lbrack \begin{array}{cc} ',sprintf('%0.2f',sigma(1,1)),' & ',sprintf('%0.2f',sigma(1,2)),' \\ ',sprintf('%0.2f',sigma(2,1)),' & ',sprintf('%0.2f',sigma(2,2)),' \end{array}\right\rbrack$']},...
    'LineStyle','none',...
    'Interpreter','latex',...
    'FitBoxToText','off');

Let's rotate the rectangle 45 degrees and compute the stresses

theta = 45
R = [cosd(theta), -sind(theta)
     sind(theta), cosd(theta)]
R = 2x2    
    0.7071   -0.7071
    0.7071    0.7071
P(:,1) = P(:,1)-1.5;
P(:,2) = P(:,2)-0.5;
P = (R*P')';
P(:,1) = P(:,1)+1.5;
P(:,2) = P(:,2)+0.5;

U = (R*U')';

U = U(:,1:2);
P = P(:,1:2);

xi = 0.5; eta = 0.5;
J = Bh(xi,eta)*P;
B = J\Bh(xi,eta);
gradU = B*U;
epsilon = 1/2*(gradU'+gradU)
epsilon = 2x2    
    0.0011    0.0022
    0.0022    0.0011
sigma = 2*mu*epsilon + lambda*trace(epsilon)*eye(2)
sigma = 2x2    
    3.6667    3.6667
    3.6667    3.6667

Principal stress

[V,D] = eig(sigma);
sigmaPrinc = diag(D);
dir = V;
dir = 2x2    
   -0.7071    0.7071
   -0.7071   -0.7071

We note that the direction dir is parallel to the rotation matrix R.

sigmaPrinc
sigmaPrinc = 2x1    
    7.3333
   -0.0000
sigma_vm = sqrt(sigma(1,1)^2-sigma(1,1)*sigma(2,2)+sigma(2,2)^2+3*sigma(1,2)^2)
sigma_vm = 7.3333

figure
patch(P(:,1),P(:,2),'w')
axis equal tight off; hold on
patch(P(:,1)+U(:,1)*20,P(:,2)+U(:,2)*20,'w','LineStyle',':', ...
    'FaceColor','none')

xm = mean(P,1);
hold on; scale = 0.3;
quiver(xm(1),xm(2),dir(1,1),dir(2,1),scale,'b','Displayname','1st principal direction')
quiver(xm(1),xm(2),-dir(1,1),-dir(2,1),scale,'b','HandleVisibility','off')
quiver(xm(1),xm(2),dir(1,2),dir(2,2),scale,'r','Displayname','2nd principal direction')
quiver(xm(1),xm(2),-dir(1,2),-dir(2,2),scale,'r','HandleVisibility','off')

annotation(gcf,'textbox',...
    [0.030 0.818 0.3 0.14],...
    'String', ...
    {['$\theta=$',sprintf(' %0.0f',theta),'$^\circ$'], ...
    ['$\sigma_1=$',sprintf(' %0.2f',sigmaPrinc(1)),'MPa'], ...
    ['$\sigma_2=$',sprintf(' %0.2f',abs(sigmaPrinc(2))),'MPa'], ...
    ['$\sigma_{vM}=$',sprintf(' %0.2f',sigma_vm),'MPa']}, ...
    'LineStyle','none', ...
    'Interpreter','latex', ...
    'FitBoxToText','off');

annotation(gcf,'textbox',...
    [0.7 0.13 0.130357139504382 0.145238091619242],...
    'String', ...
    {['$\sigma =\left\lbrack \begin{array}{cc} ',sprintf('%0.2f',sigma(1,1)),' & ',sprintf('%0.2f',sigma(1,2)),' \\ ',sprintf('%0.2f',sigma(2,1)),' & ',sprintf('%0.2f',sigma(2,2)),' \end{array}\right\rbrack$']},...
    'LineStyle','none',...
    'Interpreter','latex',...
    'FitBoxToText','off');

Example 2 - Linear triangles

P = [0.1 0.5
     0.5 0.8
     0.6 0.3];
U = [1 -1
     2 -1
     0 -2]/50;

Compute the stress matrix, von Mises stress and principal stresses for the element. Let E=22000MPaE=22000\textrm{MPa}, ν=0.3\nu =0.3. Use plane stress.

E = 22000; %MPa
nu = 0.3;
lambda = E*nu/(1-nu^2);
mu = E/(2*(1+nu));

Basis functions

phi = @(xi,eta)[1-xi-eta, xi, eta];
Bh = @(xi,eta)[-1 1 0
               -1 0 1];
B=J−1B^  \mathbf{B}=\bm J ^{-1} \hat{\mathbf{B} } \; J=B^  P\bm J =\hat{\mathbf{B} } \;\mathbf{P} 
xi = 1/3; eta = 1/3; % Does not matter for linear elements
J = Bh(xi,eta)*P
J = 2x2    
    0.4000    0.3000
    0.5000   -0.2000
B = J\Bh(xi,eta)
B = 2x3    
   -2.1739    0.8696    1.3043
   -0.4348    2.1739   -1.7391

Gradient of uu

∇u≈∇U=[∂Ux  ∂x∂Uy  ∂x∂Ux  ∂y∂Uy  ∂y]=B  U \def\arraystretch{2.5} \nabla \bm u\approx \nabla \mathbf{U}=\left\lbrack \begin{array}{cc} \dfrac{\partial U_x \;}{\partial x} & \dfrac{\partial U_y \;}{\partial x}\\ \dfrac{\partial U_x \;}{\partial y} & \dfrac{\partial U_y \;}{\partial y} \end{array}\right\rbrack =\mathbf{B}\;\mathbf{U} 
gradU = B*U
gradU = 2x2    
   -0.0087   -0.0261
    0.0783    0.0348
ε=[∂ux  ∂x12(∂ux  ∂y+∂uy  ∂x)12(∂ux  ∂y+∂uy  ∂x)∂uy∂y]=12(∇uT+∇u) \def\arraystretch{2.5} \bm \varepsilon =\left\lbrack \begin{array}{cc} \dfrac{\partial u_x \;}{\partial x} & \dfrac{1}{2}\left(\dfrac{\partial u_x \;}{\partial y}+\dfrac{\partial u_y \;}{\partial x}\right)\\ \dfrac{1}{2}\left(\dfrac{\partial u_x \;}{\partial y}+\dfrac{\partial u_y \;}{\partial x}\right) & \dfrac{\partial u_y }{\partial y} \end{array}\right\rbrack =\dfrac{1}{2}\left(\nabla \bm u^T +\nabla \bm u\right) 
epsilon = 1/2*(gradU'+gradU)
epsilon = 2x2    
    0.0031    0.0015
    0.0015    0.0009
σ=2με+λtrεI\bm \sigma =2\mu \bm \varepsilon +\lambda \textrm{tr} \bm \varepsilon \bm I 
sigma = 2*mu*epsilon + lambda*trace(epsilon)*eye(2)
sigma = 2x2    
   81.8048   24.9527
   24.9527   45.3354

Principal stresses

[V,D] = eig(sigma);
sigmaPrinc = diag(D);
dir = V;
dir = 2x2    
   -0.8916    0.4528
   -0.4528   -0.8916
sigmaPrinc
sigmaPrinc = 2x1    
   94.4755
   32.6647

figure
patch(P(:,1),P(:,2),'w')
axis equal; hold on
patch(P(:,1)+U(:,1),P(:,2)+U(:,2),'w','LineStyle','--', ...
    'FaceColor','none')

xm = mean(P,1);
quiver(xm(1),xm(2),dir(1,1),dir(1,2),0.4,'Color','b')
quiver(xm(1),xm(2),dir(2,1),dir(2,2),0.4,'Color','r')

Example 3 - Quadrilateral

P = [0 0
     1 -0.1
     1.2 1
     -0.1, 1.2];
U = [1 -5
     -1 -5
     -1 5
     1 5]/50;

Let E=2100,ν=0.33E=2100,\nu =0.33.

The basis functions for the quadrilateral are given by:

phi = @(xi,eta)[(eta-1.0).*(xi-1.0),-xi.*(eta-1.0),eta.*xi,-eta.*(xi-1.0)];
Bh = @(xi,eta)[eta-1, 1-eta, eta, -eta;
               xi-1,  -xi,   xi,  1-xi ];

Material data

E = 2200; %MPa
nu = 0.33;

%Plane Stress
lambda = E*nu/(1-nu^2);
mu = E/(2*(1+nu));

Stresses are super convergent at Gauss points, see e.g., Cook Section 6.10 in [1].

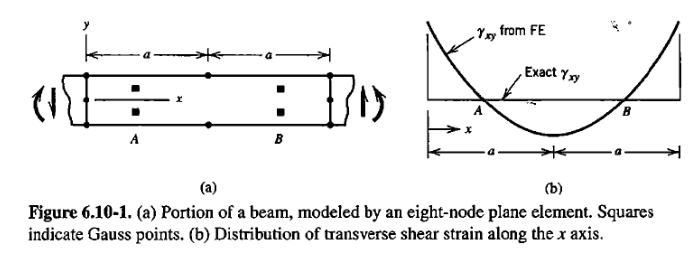
Loop over all Gauss points.

figure
patch(P(:,1),P(:,2),'w')
axis equal; hold on

order = 2;
[GP,GW] = GaussQuadrilateral(order);

for ig = 1:4
    xi = GP(ig,1);
    eta = GP(ig,2);
    
    J = Bh(xi,eta)*P;
    B = J\Bh(xi,eta);
    gradU = B*U;
    epsilon = 1/2*(gradU'+gradU);
    sigma = 2*mu*epsilon + lambda*trace(epsilon)*eye(2);
    sigma_vm = sqrt(sigma(1,1)^2-sigma(1,1)*sigma(2,2)+sigma(2,2)^2+3*sigma(1,2)^2);

    iP = phi(xi,eta)*P;
    text(iP(1),iP(2),num2str(sigma_vm))
end

Loop over all nodes.

Ph = [0 0
      0 1
      1 1
      1 0];
for ig = 1:4
    xi = Ph(ig,1); eta = Ph(ig,2);
    
    J = Bh(xi,eta)*P;
    B = J\Bh(xi,eta);
    gradU = B*U;
    epsilon = 1/2*(gradU'+gradU);
    sigma = 2*mu*epsilon + lambda*trace(epsilon)*eye(2);
    sigma_vm = sqrt(sigma(1,1)^2-sigma(1,1)*sigma(2,2)+sigma(2,2)^2+3*sigma(1,2)^2);

    iP = phi(xi,eta)*P;
    text(iP(1),iP(2),num2str(sigma_vm))
end

Nodal averaging - L2L_2 projection

If we want to take a field that exists inside the element and interpolate it to the nodes, we basically want to minimize

J(uh)=12∫Ω(u−uh)2J\left(\bm u_h \right)=\dfrac{1}{2}\sqrt{\int_{\Omega } {\left(\bm u - \bm u_h \right)}^2 }

where uh\bm u_h is the nodal field and u\bm u the element field. This yields the best average in L2L_2. The problem states: Find uh\bm u_h such that

∫Ω(u−uh)vdΩ=0⇒∫ΩuvdΩ=∫ΩuhvdΩ\int_{\Omega } \left(\bm u - \bm u_h \right) \bm v d\Omega = 0 \Rightarrow \int_{\Omega } \bm u \bm v d\Omega =\int_{\Omega } \bm u_h \bm v d\Omega

Apply Galerkin and approximate uh≈∑iφiui  u_h \approx \sum_i \varphi_i u_i \; which leads to

∫Ωφiφj  dΩ  ui=∫Ωuφj  dΩ\int_{\Omega } \varphi_i \varphi_j \;d\Omega \;u_i =\int_{\Omega } u\varphi_j \;d\Omega

or

M  u=b\mathbf{M}\;\mathbf{u}=\mathbf{b}

For our example, using one bi-linear element, we have the von Mises stress in each Gauss point which we want to interpolate to the nodes, so

be=∫KφT(ξi,ηi)σvM,i  d  K≈∑i=14φT(ξi,ηi)σvM,i  det⁡(Ji)dK^wi{\mathit{\mathbf{b} } }_e =\int_K \varphi^T \left(\xi_i ,\eta_i \right)\sigma_{\textrm{vM},i} \;d\;K\approx \sum_{i=1}^4 \varphi^T \left(\xi_i ,\eta_i \right)\sigma_{\textrm{vM},i} \;\det \left(J_i \right){d\hat{\mathrm{K} } w}_i

and

Me=∫KφT(ξi,ηi)φ(ξi,ηi)d  K≈∑i=14φT(ξi,ηi)φ(ξi,ηi)  det⁡(Ji)dK^wiM_e =\int_K \varphi^T \left(\xi_i ,\eta_i \right)\varphi \left(\xi_i ,\eta_i \right)d\;K\approx \sum_{i=1}^4 \varphi^T \left(\xi_i ,\eta_i \right)\varphi \left(\xi_i ,\eta_i \right)\;\det \left(J_i \right){d\hat{\mathrm{K} } w}_i

where dK^d\hat{\mathrm{K} } is the area of the reference element. Thus we can get

σvMn=Me−1be\sigma_{\textrm{vMn} } ={\mathit{\mathbf{M} } }_e^{-1} {\mathit{\mathbf{b} } }_e

Let's implement this in Matlab, loop over all Gauss points

order = 2;
[GP,GW] = GaussQuadrilateral(order);

Me = zeros(4,4);
be = zeros(4,1);
for ig = 1:4
    xi = GP(ig,1); eta = GP(ig,2); iW = GW(ig);
    
    J = Bh(xi,eta)*P;
    B = J\Bh(xi,eta);
    gradU = B*U;
    epsilon = 1/2*(gradU'+gradU);
    sigma = 2*mu*epsilon + lambda*trace(epsilon)*eye(2);
    sigma_vm = sqrt(sigma(1,1)^2-sigma(1,1)*sigma(2,2)+sigma(2,2)^2+3*sigma(1,2)^2);

    iP = phi(xi,eta)*P;
    Me = Me + phi(xi,eta)'*phi(xi,eta)*det(J)*1*iW;
    be = be + phi(xi,eta)'*sigma_vm*det(J)*1*iW;
end
sigma_vmn = Me\be
sigma_vmn = 4x1    
   31.3527
   35.2472
   34.9635
   31.9640
scale = 1;
figure; 
patch(P(:,1)+U(:,1)*scale,P(:,2)+U(:,2)*scale,'w','LineStyle','-', ...
    'FaceColor','interp','Cdata',sigma_vmn)
axis equal 
colorbar
colormap jet
title('von Mises stress')

Example 4 - Nodal averaging a triangular mesh

We start by creating the geometry using the Partial Differential Toolbox.

clear
R1 = [3,4,0,20,20,0,0,0,8,8]'; %Create a rectangle
C1 = [4,10,5,2,2]'; %Create a circle in the middle with radius 0.3

C1 and R1 need to be concatenated so one of them needs to be increased with zeros.

C1 = [C1;zeros(length(R1)-length(C1),1)];

gd holds the geometric description.

gd = [R1,C1];
sf = 'R1-C1'; % Here we remove C1 from R1.
% sf = 'R1'; % Nothing is removed
ns = char('R1','C1')'; % Label the geometric entities, so we know which is which.
g = decsg(gd,sf,ns);

g holds the primitive geometries lines, and arc segments to describe any 2D geometry.

model = createpde;
geometryFromEdges(model,g);

figure
pdegplot(model,'EdgeLabels','on')
axis tight

Solve the static linear elasticity PDE using linear elements.

{−∇⋅σ=fin    Ωσ=2με+λtrεIin  Ωσ⋅n=Fton  E1uy=0on  E4ux=0on  E3n\left\lbrace \begin{array}{ll} -\nabla \cdot \sigma =f & \textrm{in}\;\;\Omega \\ \sigma =2\mu \varepsilon +\lambda \textrm{tr}\varepsilon I & \textrm{in}\;\Omega \\ \sigma \cdot n=F_t & \textrm{on}\;E_1 \\ u_y =0 & \textrm{on}\;E_4 \\ u_x =0 & \textrm{on}\;E_3 n \end{array}\right.

Let E=210000MPa,E=210000\textrm{MPa}, ν=0.33\nu =0.33, t=0.6  mmt=0.6\;\textrm{mm}, the height H=8H=8 mm, the width W=20W=20 mm, the traction force Ft=5000/(Ht) N/mm2F_t=5000 / (H t) \text{ N/mm}^2 use plane stress and implement a solver to numerically find the displacement field and compute the nodal averaged von Mises stress field and the nodal averaged principle stress and its directions.

Solution

We start by creating the mesh

h = 1 %mm Overall mesh size

Here we can use Hedge as a mesh control, in this case we set the mesh size of edge 8,7,5 and 6 to 0.3. The parameter hgrad means how much an element can grow in size from one element to the next.

mesh = generateMesh(model, 'Hmax', h, 'Hmin', h/2,...
    'hgrad',1.5, 'GeometricOrder', 'linear', 'Hedge',{8,0.3,7,0.3,5,0.3,6,0.3});

Next we set the material parameters and thickness of the geometry

E = 210000; %MPa
nu = 0.33;
t = 0.6; %mm

% Plane Stress
lambda = E*nu/(1-nu^2);
mu = E/(2*(1+nu));

The load case is established next

P = mesh.Nodes';
nodes = mesh.Elements';
[nele, knod] = size(nodes);
[nnod, dof] = size(P);
neq = nnod*dof;

H = max(P(:,2))-min(P(:,2))    %mm
traction = [5000/(H*t),0]' % traction load N/mm^2
edge = 1; % The edge on which the load is applied

% Here we compute the traction load and the stiffness matrix
F = TractionLoad(mesh,t,traction,edge);
S = LinElastStiffness(mesh, lambda, mu, t);

% Visualize the mesh
figure; hold on
patch('Vertices', P, 'Faces', nodes,'FaceColor', 'c', ...
    'EdgeAlpha',0.1,'DisplayName','linear mesh')
axis equal tight

% Visualize the load
Finds = findNodes(mesh,'region','Edge',edge);
quiver(P(Finds,1), P(Finds,2), F(Finds*2-1), F(Finds*2-0),'b', ...
    'DisplayName','F=[5000,0]N');

% Apply essential boundary conditions in x-dir
u = zeros(neq,1);
%E1 = findNodes(mesh,'region','Edge',4);
E1 = findNodes(mesh,'nearest',[0;0]) % Get the node at point (0,0) 
% Prescribe displacements
u(E1*2) = 0; %y-displacements

% Visualize the boundary conditions in y-dir
plot(P(E1,1),P(E1,2),'bd','MarkerFaceColor','b','Displayname','u_y=0')

% Apply essential boundary conditions in y-dir
E4 = findNodes(mesh,'region','Edge',3);
% prescribed displacement
u(E4*2-1) = 0; %x-displacements

% Visualize the boundary conditions in x-dir
plot(P(E4,1),P(E4,2),'rs','MarkerFaceColor','r','Displayname','u_x=0')

hl = legend('show'); 
set(hl,'Position',[0.60 0.69 0.20 0.20]);

Apply boundary conditions and solve for the unknown displacement.

presc = unique([E4*2-1, E1*2]);
free = setdiff(1:neq,presc);

F = F - S(:,presc)*u(presc);
u(free) = S(free,free)\F(free);

Visualize the resulting displacement field

U = [u(1:2:end), u(2:2:end)];
UR = sum(U.^2,2).^0.5;
scale = 3;
figure; hold on
pdegplot(model,'EdgeLabels','off')
patch('Vertices', P+U*scale, 'Faces', nodes,'FaceColor', 'interp', ...
    'EdgeAlpha',0.1,'CData',UR)
axis equal tight
title(['Displacement field, scale: ',num2str(scale)])

Verification of the model

We verify the displacements first. Use a simple geometry for verification and then change the geometry once the model is verified.

∑Fi=Ftraction  A \sum F_i =F_{\mathrm{traction}} \;A 
sum(F)                         %N
W = max(P(:,1))-min(P(:,1))    %mm
H = max(P(:,2))-min(P(:,2))    %mm
A = t*H                        %mm^2  Cross sectional area
f = traction(1)*A              %N     Total external load
deltax = f*W/(E*A)             %mm    Total x deformation
epsx = deltax/W                %mm/mm Strain in x-dir
epsy = -nu*(epsx)              %mm/mm Strain in y-dir
deltay = epsy*H                %mm    Total y deformation

sigma_nominal = f/A            %N/mm^2 or MPa stress

ux = max(U(findNodes(mesh,'region','Edge',1),1))
uy = min(U(findNodes(mesh,'region','Edge',2),2))

Without the hole we get:

sum(F) = 5000
W = 20
H = 8
A = 4.0
f = 5000
deltax = 0.0992
epsx = 0.0050
epsy = -0.0016
deltay = -0.0131

sigma_nominal = 1.0417e+03

ux = 0.0992
uy = -0.0131

Computing the stress

phi = @(xi,eta)[1-xi-eta, xi, eta];
Bh = [-1,1,0
      -1,0,1];

GP = [0.5  0
      0.5  0.5
      0    0.5];
GW = [1/3, 1/3, 1/3];

% Alternative Gauss points
% GP = [1/6 1/6
%       2/3 1/6
%       1/6 2/3];
% GW = 1/3*[1;1;1];

Dir1 = zeros(nele,2);
Dir2 = zeros(nele,2);
sigma_vmE = zeros(nele,1);
Xm = zeros(nele,2);

Sig1 = zeros(nnod,1);
Sig2 = zeros(nnod,1);

M = zeros(nnod,nnod);
b = zeros(nnod,1);
for iel = 1:nele
    inod = nodes(iel,:);
    
    iP = P(inod,:);
    iU = U(inod,:);

    J = Bh*iP;
    area = det(J)*1/2;

    B = J\Bh;
    gradU = B*iU;
    epsilon = 1/2*(gradU'+gradU); % Verify these by comparing the epsx and epsy
    sigma = 2*mu*epsilon + lambda*trace(epsilon)*eye(2); % Verify by comparing to sigma_nominal
    sigma_vm = sqrt(sigma(1,1)^2-sigma(1,1)*sigma(2,2)+sigma(2,2)^2+3*sigma(1,2)^2);
    
    [V,D] = eig(sigma, 'vector');
    dir = V;
    Dir1(iel,:) = dir(:,1);
    Dir2(iel,:) = dir(:,2);
    sigmaPrinc= D(ind);
    sig1 = sigmaPrinc(1);
    sig2 = sigmaPrinc(2);

    Xm(iel,:) = mean(iP,1)+mean(iU)*scale;

    sigma_vmE(iel) = sigma_vm;

    xi = 1/3; eta = 1/3; iw = 1;
    b(inod) = b(inod) + phi(xi,eta)'*sigma_vm*area*iw;
    Sig1(inod) = Sig1(inod) + phi(xi,eta)'*sig1*area*iw;
    Sig2(inod) = Sig2(inod) + phi(xi,eta)'*sig2*area*iw;

    Me = zeros(3,3); be = zeros(3,1);
    for ig = 1:3
        xi = GP(ig,1); eta = GP(ig,2);
        iw = GW(ig);
        Me = Me + phi(xi,eta)'*phi(xi,eta)*area*iw;
    end

    M(inod,inod) = M(inod,inod) + Me;

end

sigma_vmn = M\b;
Sig1 = M\Sig1;
Sig2 = M\Sig2;

figure
patch('Faces',nodes,'Vertices',P+U*scale, 'EdgeAlpha', 0.2, ...
    'FaceColor','flat','CData',sigma_vmE)
axis equal off; hold on;
title('von Mises stress, element values')
colorbar; colormap jet
caxis([0, max(sigma_vmE)])
max(sigma_vmE)
ans = 5.4222e+03
figure
patch('Faces',nodes,'Vertices',P+U*scale, 'EdgeAlpha', 0.2, ...
    'FaceColor','interp','CData',sigma_vmn)
axis equal off; hold on;
title('von Mises stress, nodal averaged')
colorbar; colormap jet
caxis([0, max(sigma_vmn)])
max(sigma_vmn)
ans = 5.3091e+03
figure
patch('Faces',nodes,'Vertices',P+U*scale, 'EdgeAlpha', 0.2, ...
    'FaceColor','interp','CData',Sig1)
axis equal off; hold on;
title('First principal stress, nodal averaged')
colorbar; colormap jet
quiver(Xm(:,1),Xm(:,2),Dir1(:,1),Dir1(:,2),0.2,'ShowArrowHead','off','Color','k')
caxis([min(Sig1), max(Sig1)])
max(Sig1)
ans = 5.5595e+03
min(Sig1)
ans = -1.6973e+03

function F = TractionLoad(mesh,t,fload,edge)
    P = mesh.Nodes';
    nodes = mesh.Elements';
    [nele, knod] = size(nodes);
    [nnod, dof] = size(P);
    neq = nnod*dof;
    
    
    phi=@(xi)[1-xi,xi];
    Einds = findNodes(mesh,'region','Edge',edge);
    
    eleInds = find(sum(ismember(nodes,Einds),2)>1);
    F = zeros(neq,1);
    ieqs = zeros(2*2,1);
    PHI = zeros(2,4);
    L = 0;
    nele = length(eleInds);
    for iel = 1:nele
        indTri = eleInds(iel);
        iTri = nodes(indTri,:);
        iEdgeNodes = iTri(ismember(iTri,Einds));
    
        ieqs(1:2:end) = 2*iEdgeNodes-1; %x-dofs
        ieqs(2:2:end) = 2*iEdgeNodes-0; %y-dofs
        xc = P(iEdgeNodes,:);
        h = norm(xc(end,:)-xc(1,:));
        L = L + h;
    
        xi = 0.5; iw = 1;
        PHI(1,1:2:end) = phi(xi);
        PHI(2,2:2:end) = phi(xi);
    
        fe = PHI'*fload(:)*t*h*iw;
    
        F(ieqs) = F(ieqs) + fe;
    end
end

function S = LinElastStiffness(mesh, lambda, mu, t)
    P = mesh.Nodes';
    nodes = mesh.Elements';

    [nele, knod] = size(nodes);
    [nnod, dof] = size(P);
    neq = nnod*dof;

    phi = @(xi,eta)[1-xi-eta, xi, eta];
    Bh = [-1,1,0
        -1,0,1];

    S = zeros(neq,neq);
    sq = 1/sqrt(2);
    for iel = 1:nele
        inod = nodes(iel,:);
        iP = P(inod,:);

        locdof = zeros(1,6);
        locdof(1:2:end) = inod*2-1;
        locdof(2:2:end) = inod*2;

        J = Bh*iP;
        area = det(J) * 1/2;

        B = J\Bh;

        Beps = zeros(3,6);
        Beps(1,1:2:end) = B(1,:);
        Beps(2,2:2:end) = B(2,:);
        Beps(3,1:2:end) = sq*B(2,:);
        Beps(3,2:2:end) = sq*B(1,:);

        Bdiv = zeros(1,6);
        Bdiv(1:2:end) = B(1,:);
        Bdiv(2:2:end) = B(2,:);

        Se = t*(2*mu*Beps'*Beps + lambda*Bdiv'*Bdiv)*area;

        S(locdof, locdof) = S(locdof, locdof) + Se;
    end

end

function [GP,GW] = GaussQuadrilateral(order)
%GaussQuadrilateral Gauss integration scheme for quadrilateral 2D element
%   [x,y] in [0,1]

[gp,gw] = gauss(order,0,1);

[GPx,GPy] = meshgrid(gp,gp);
[Gw1,Gw2] = meshgrid(gw,gw);
GW = [Gw1(:), Gw2(:)];
GW = prod(GW,2);
GP = [GPx(:), GPy(:)];

end

function [x, w, A] = gauss(n, a, b)
%------------------------------------------------------------------------------
% gauss.m
%------------------------------------------------------------------------------
%
% Purpose:
%
% Generates abscissas and weights on I = [ a, b ] (for Gaussian quadrature).
%
%
% Syntax:
%
% [x, w, A] = gauss(n, a, b);
%
%
% Input:
%
% n    integer    Number of quadrature points.
% a    real       Left endpoint of interval.
% b    real       Right endpoint of interval.
%
%
% Output:
%
% x    real       Quadrature points.
% w    real       Weigths.
% A    real       Area of domain.
%------------------------------------------------------------------------------
% 3-term recurrence coefficients:
n = 1:(n - 1);
beta = 1 ./ sqrt(4 - 1 ./ (n .* n));
% Jacobi matrix:
J = diag(beta, 1) + diag(beta, -1); 
% Eigenvalue decomposition:
%
% e-values are used for abscissas, whereas e-vectors determine weights.
%
[V, D] = eig(J);
x = diag(D);
% Size of domain:
A = b - a;
% Change of interval:
%
% Initally we have I0 = [ -1, 1 ]; now one gets I = [ a, b ] instead.
%
% The abscissas are Legendre points.
%
if ~(a == -1 && b == 1)
  x = 0.5 * A * x + 0.5 * (b + a);
end
% Weigths:
w = V(1, :) .* V(1, :);
end

References

[1]
R. D. Cook, D. S. Malkus, M. E. Plesha, and R. J. Witt, Concepts and applications of finite element analysis, 4th edition, 4th ed. Wiley, 2001.
© Mirza Cenanovic. Last modified: January 17, 2024. Website built with Franklin.jl and the Julia programming language.