Download this page as a Matlab LiveScript
Table of contents
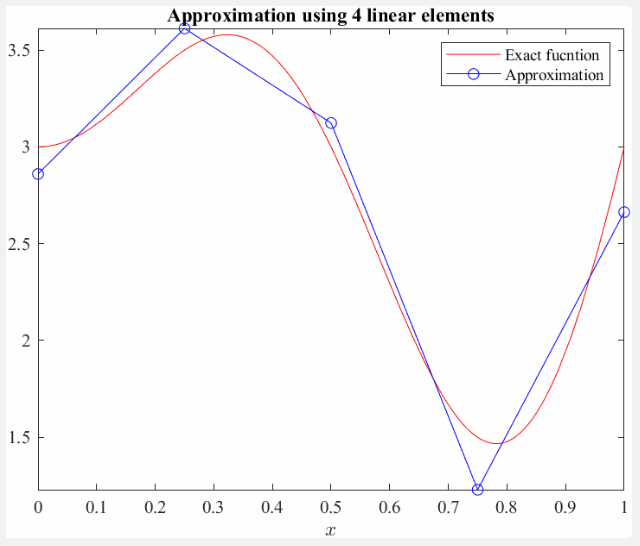
So we want to approximate the function
\[u\left(x\right)=2x\;\sin \left(2\pi x\right)+3\;\textrm{for}\;x\in \left\lbrack 0,1\right\rbrack\]using piecewise elements of order 1 or 2.
This means finding all nodal values \(u_i\) to the approximation (the blue circles in the figure above). This problem can be formulated using Galerkin as such: Find \(u_i\) such that
\[\int_{0}^{1}r(x,u_{i})\varphi_{i}dx=0\] \[=\int_0^1 \left(U\left(x,u_i\right) - u\left(x\right)\right)\varphi_j \;d\;x\;=0\]with \(U\left(x,u_i\right)=\sum_i \varphi_i \left(x\right){u}_i\)
Now, this is the same old Galerkin expression as we had in the previous section. In order to apply a piecewise approximation, we shall further expand the expressions to formulate a matrix system!
Expanding the expression in the integral we get
\[\int_0^1 \left(\sum_i \varphi_i \left(x\right)\varphi_j \left(x\right){\;u}_i -u\left(x\right)\varphi_j \left(x\right)\right)\;d\;x\;=0\] \[=\int_0^1 \sum_i \varphi_i \left(x\right)\varphi_j \left(x\right){\;u}_i \;d\;x-\int_0^1 u\left(x\right)\varphi_j \left(x\right)\;d\;x=0\]move \(u_i \;\)out
\[\sum_i \int_0^1 \varphi_i \left(x\right)\varphi_j \left(x\right)\;d\;x\;\;{\;u}_i =\int_0^1 u\left(x\right)\varphi_j \left(x\right)\;d\;x\]which is equivalent to the matrix system
\(M_{\textrm{ij} } u_i =f_i\) or \(\mathit{\mathbf{M} }\;\mathit{\mathbf{u} }=\mathit{\mathbf{f} }\)
Solving this system gets us all nodal values for \(u_i\).
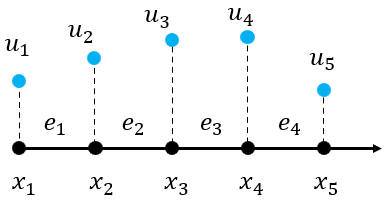
To describe any mesh we need a coordinate matrix (vector in 1D)
\[ \mathbf{x}=\begin{bmatrix}x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ x_{5} \end{bmatrix} \]and a nodal connectivity matrix
\[ \mathbf{T}=\begin{bmatrix}1 & 2\\ 2 & 3\\ 3 & 4\\ 4 & 5 \end{bmatrix} \]4 linear elements will lead to 5 equations to be solved for \(u_i ,i=1,2,\ldotp \ldotp \ldotp ,5\)
\[ \mathbf{u}=\begin{bmatrix}u_{1}\\ u_{2}\\ u_{3}\\ u_{4}\\ u_{5} \end{bmatrix} \]An element \(e\) between nodes \(x_i\) and \(x_j\) contributes only to equations \(i\;\)and \(j\). We can use the \(e\)'th row of \(\mathbf T\) to see which nodes are associated with the element \(e\).
Example: Element mass matrix for element 3 between node 3 and 4:
We can use local node numbering to simplify things:
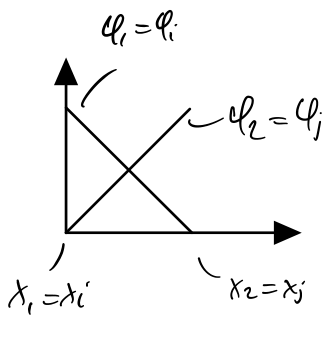
Now, for each element \(e\) we define \(x_1\) and \(x_2\), compute \(\varphi\) and then compute \(\mathbf{M}^e\) and \(\mathbf{f}^e\)
Element stiffness matrix
\[\mathbf{M}^e =\int_{x_1 }^{x_2 } \boldsymbol\varphi^T \boldsymbol\varphi dx\]or
\[ \def\arraystretch{2.5} \mathbf{M}^{e}=\begin{bmatrix}\int_{x_{1}}^{x_{2}}\varphi_{1}\varphi_{1} \;dx & \int_{x_{1}}^{x_{2}}\varphi_{1}\varphi_{2} \;dx\\ \int_{x_{1}}^{x_{2}}\varphi_{2}\varphi_{1} \;dx & \int_{x_{1}}^{x_{2}}\varphi_{2}\varphi_{2} \;dx \end{bmatrix} \]and element load vector
\[\mathbf{f}^e =\int_{x_1 }^{x_2 } \varphi^T u(x) \;dx\]or
\[ \def\arraystretch{2.0} \mathbf{f}^e =\left\lbrack \begin{array}{c} \int_{x_1 }^{x_2 } u(x) \varphi_1 \;dx\\ \int_{x_1 }^{x_2 } u(x) \varphi_2 \;dx \end{array}\right\rbrack \]Utilizing a piecewise approximation leads to the element mass matrix and element load vector:
\[M_e =\int_{x_1 }^{x_2 } {\varphi }^T \varphi \;d\;x\]and
\[f_e =\int_{x_1 }^{x_2 } {\varphi }^T u\left(x\right)\;d\;x\]which need to be assembled into the global mass matrix and load vectors.
For each element \(e\), we add \(\mathbf{M}^e\) and \(\mathbf{f}^e\) to the correct place in \(\mathbf{M}\) and \(\mathbf{f}\).
Element 1: M([1,2],[1,2])
Element 2: M([2,3],[2,3])
Element 3: M([3,4],[3,4])
Element 4: M([4,5],[4,5])
We need to add each element contribution to the global mass matrix.
or on matrix form
where row denotes the array containing the row indices and col the column indices. Thus we could write
to mean a sub-matrix of \(M\) with rows \(i\) and \(j\) and columns \(i\) and \(j\).
The corresponding Matlab (or Julia) syntax is
M([i,j],[i,j]) = M([i,j],[i,j]) + MeAll nodes that have several elements will get contributions from each element. We are "accumulating" mass to these nodes from the elements.
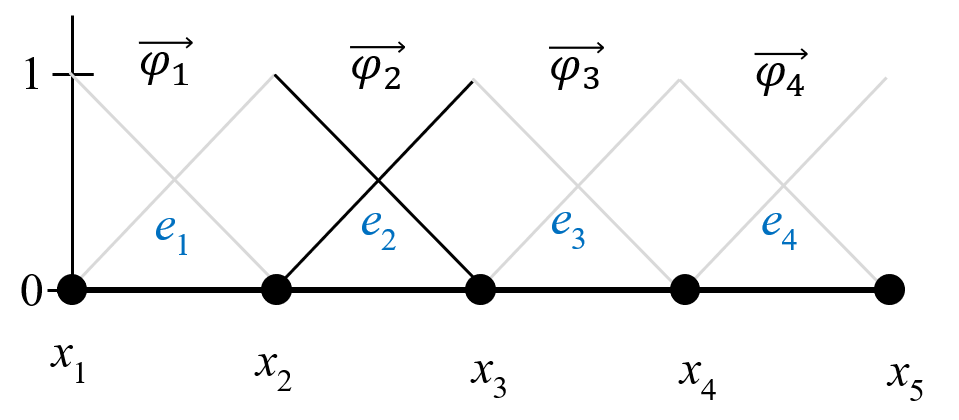
Contribution from element 1
Contribution from element 2
etc
For four linear elements, this leads to the equation system
\[ \left(\begin{array}{c} 0.083\,u_1 +0.042\,u_2 =0.39\\ 0.042\,u_1 +0.17\,u_2 +0.042\,u_3 =0.85\\ 0.042\,u_2 +0.17\,u_3 +0.042\,u_4 =0.72\\ 0.042\,u_3 +0.17\,u_4 +0.042\,u_5 =0.45\\ 0.042\,u_4 +0.083\,u_5 =0.27 \end{array}\right) \]We end up with the linear system of equations
\[ \mathbf{Mu=f} \]which is solved by using a linear equations solver, in Matlab we do this by
u = M\fWe will do this in code now using linear element and symbolic integration.
clear
syms x
ue(x) = 2*x*sin(2*pi*x)+3;
N = 4;
nnod = N+1;
xnod = linspace(0,1,N+1);
nodes = [(1:nnod-1)', (2:nnod)'];
Phi = @(x,x1,x2) [(x2-x)/(x2-x1), (x-x1)/(x2-x1)];
M = zeros(nnod,nnod); F = zeros(nnod,1);
for iel = 1:N
inod = nodes(iel,:);
xc = xnod(inod);
x1 = xc(1); x2 = xc(2);
phi = @(x)Phi(x,x1, x2);
Me = int(phi(x).'*phi(x), x,x1,x2);
fe = int(phi(x).'*ue(x), x,x1,x2);
M(inod,inod) = M(inod,inod) + Me;
F(inod) = F(inod) + fe;
end
u = M\F;
figure
fplot(ue,[0,1],'r','LineWidth',2); hold on
plot(xnod,u,'-bo')
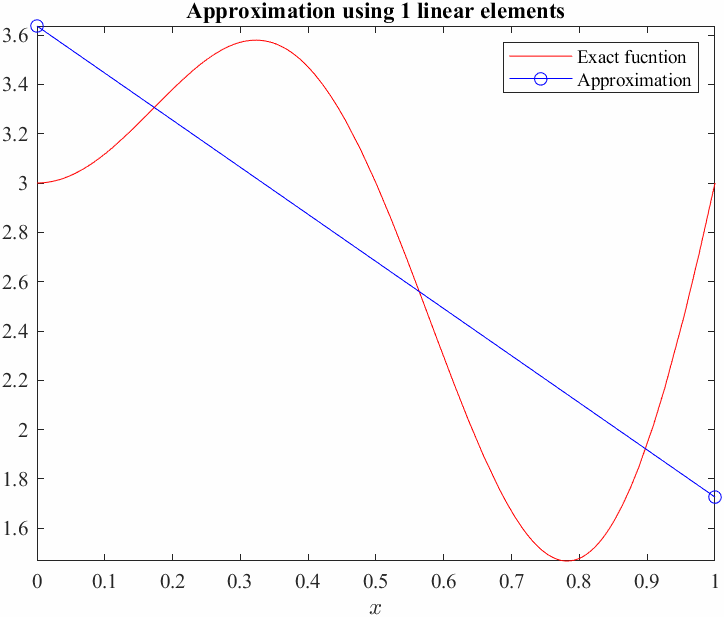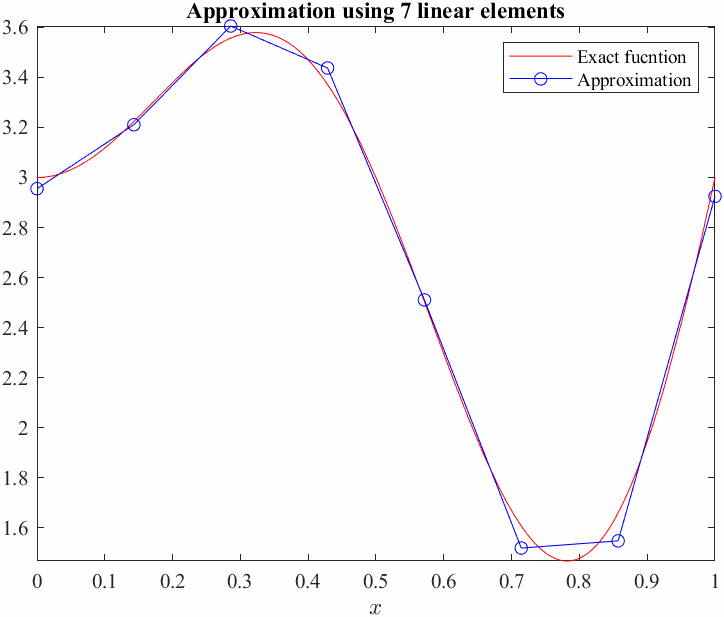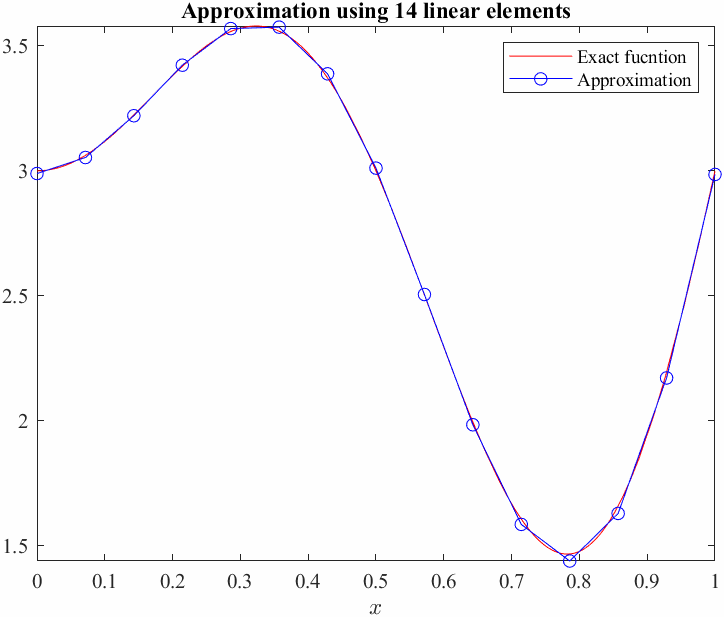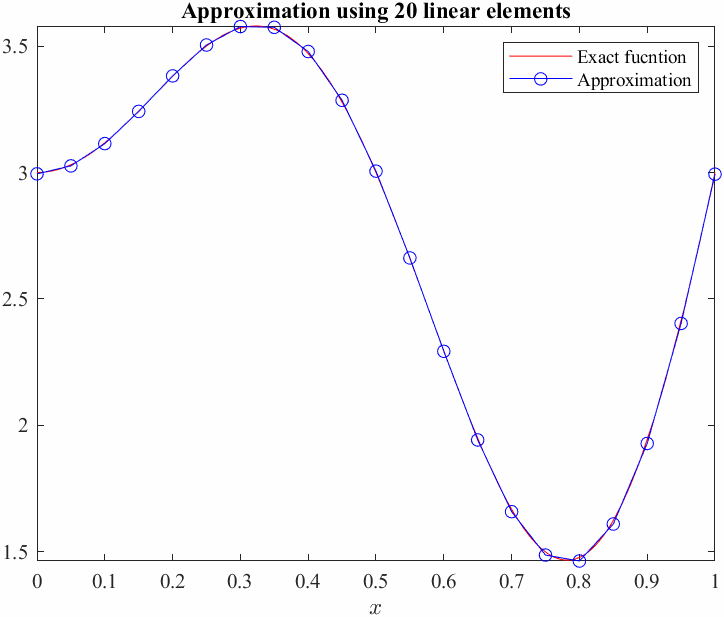
Now, we will compute the average error between the exact function and our Galerkin approximation, we shall use the \(L_2\) norm as a measure of error. This basicaly means squaring the difference between the functions over the entire domain and taking the square root.
\[L_2 \textrm{error}:=\sqrt{\int_0^1 {\left(U-u\right)}^2 \;d\;x}\]So we need to compute the difference between the function for each element and adding it all up.
\[L_2 \textrm{error}:=\sqrt{\int_0^1 {\left(U-u\right)}^2 \;d\;x}=\sqrt{\sum_e^N \int_e^{\;} {\left(U_e -u\right)}^2 \;d\;x}\]where
\[U_e \left(x\right)=\varphi \left(x\right){\mathit{\mathbf{u} } }_e \overset{\textrm{lin}\;\textrm{ele} }{=} \left\lbrack \begin{array}{cc} \varphi_1 & \varphi_1 \end{array}\right\rbrack \left\lbrack \begin{array}{c} u_1 \\ u_2 \end{array}\right\rbrack\]L2err = 0;
for iel = 1:N
inod = nodes(iel,:);
x1 = xnod(inod(1)); x2 = xnod(inod(2));
phi = @(x)Phi(x,x1, x2);
U = phi(x)*u(inod);
L2err = L2err + double(int((U-ue)^2, x,x1,x2));
end
L2err = sqrt(L2err)L2err = 0.1106Now we can start changing \(N\) to see how the error goes down. If we plot \(N\) versus the error we get a convergence plot.
clear
syms x
ue(x) = 2*x*sin(2*pi*x)+3;
NN = [2,4,8,16,32];
L2Err = [];
Time = [];
figure
fplot(ue,[0,1],'r','LineWidth',2); hold on
hp = plot(NaN,NaN,'-b.');
for N = NN
tic
nnod = N+1;
xnod = linspace(0,1,N+1);
nodes = [(1:nnod-1)', (2:nnod)'];
Phi = @(x,x1,x2) [(x2-x)/(x2-x1), (x-x1)/(x2-x1)];
M = zeros(nnod,nnod); F = zeros(nnod,1);
for iel = 1:N
inod = nodes(iel,:);
xc = xnod(inod);
x1 = xc(1); x2 = xc(2);
phi = @(x)Phi(x,x1, x2);
Me = vpaintegral(phi(x).'*phi(x), x,x1,x2);
fe = vpaintegral(phi(x).'*ue(x), x,x1,x2);
M(inod,inod) = M(inod,inod) + Me;
F(inod) = F(inod) + fe;
end
u = M\F;
t1 = toc;
Time(end+1) = t1;
L2err = 0;
for iel = 1:N
inod = nodes(iel,:);
x1 = xnod(inod(1)); x2 = xnod(inod(2));
phi = @(x)Phi(x,x1, x2);
U = phi(x)*u(inod);
L2err = L2err + double(vpaintegral((U-ue)^2, x,x1,x2));
end
L2err = sqrt(L2err);
L2Err(end+1) = L2err;
set(hp,'XData',xnod, 'YData',u);
title(sprintf("Approximation using %d linear elements",N))
pause(0.1)
drawnow
end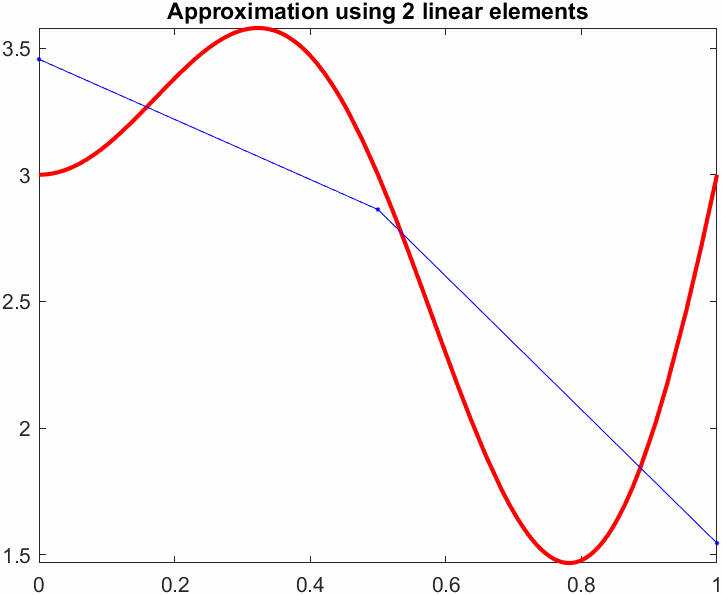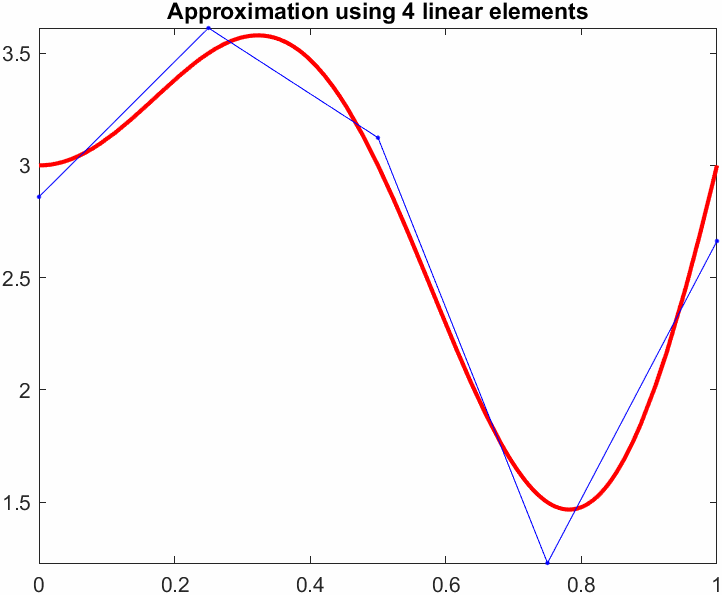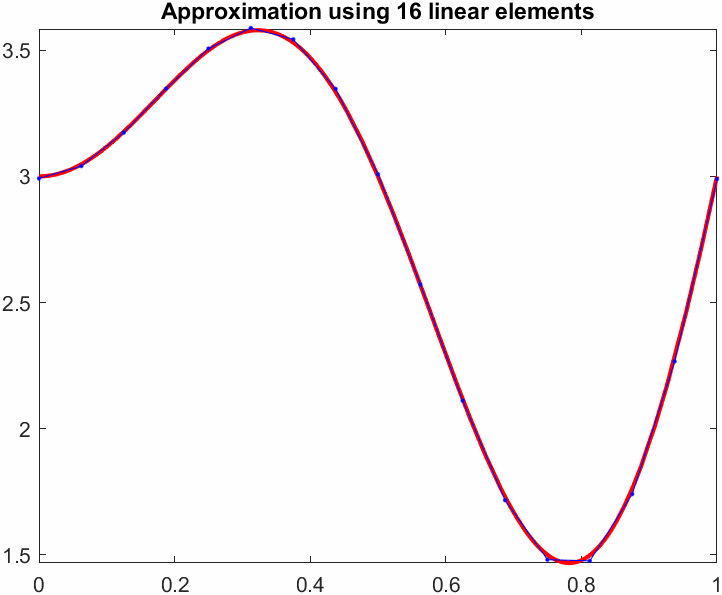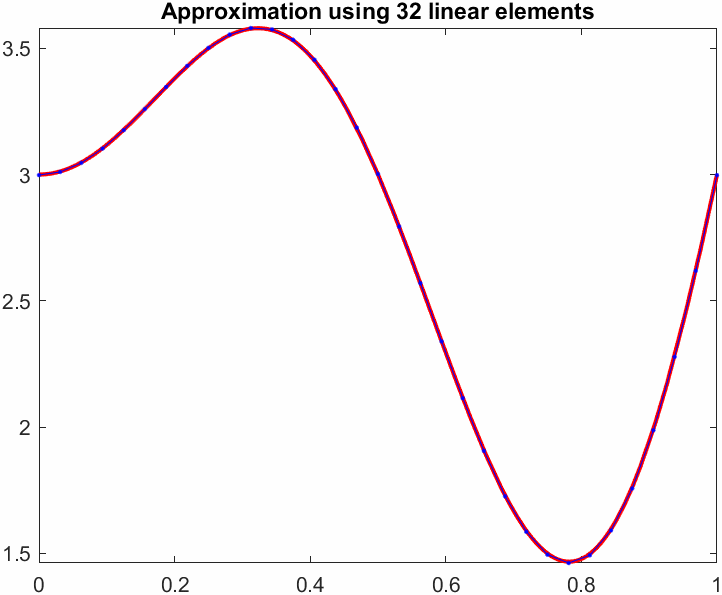
syms x1 x2 x3 x
A = [1 x1 x1^2
1 x2 x2^2
1 x3 x3^2];
C = A\eye(3);
Phi = simplify([1 x x^2]*C);
Phi = matlabFunction(Phi);
Time2 = []; L2Err2 = [];
figure;
for N = NN
tic
nnod = N*2+1;
xnod = linspace(0,1,nnod);
nodes = [(1:2:nnod-2)', (2:2:nnod-1)', (3:2:nnod)'];
neq = nnod*1;
M = zeros(nnod,nnod); F = zeros(nnod,1);
for iel = 1:N
inod = nodes(iel,:);
xc = xnod(inod);
x1 = xc(1); x2 = xc(2); x3 = xc(3);
phi = @(x)Phi(x,x1, x2, x3);
Me = vpaintegral(phi(x).'*phi(x), x,x1,x3);
fe = vpaintegral(phi(x).'*ue(x), x,x1,x3);
M(inod,inod) = M(inod,inod) + Me;
F(inod) = F(inod) + fe;
end
u = M\F;
t1 = toc;
Time2(end+1) = t1;
L2err = 0;
for iel = 1:N
inod = nodes(iel,:);
xc = xnod(inod);
x1 = xc(1); x2 = xc(2); x3 = xc(3);
phi = @(x)Phi(x,x1, x2, x3);
U = phi(x)*u(inod);
L2err = L2err + double(vpaintegral((U-ue)^2, x,x1,x3));
end
L2err = sqrt(L2err);
L2Err2(end+1) = L2err;
clf
fplot(ue,[0,1],'r','LineWidth',1);
hold on
for iel = 1:N
inod = nodes(iel,:);
xc = xnod(inod);
x1 = xc(1); x2 = xc(2); x3 = xc(3);
phi = @(x)Phi(x,x1, x2, x3);
U = phi(x)*u(inod);
fplot(U, [x1,x3])
plot(xc,u(inod),'.b');
end
title(sprintf("Approximation using %d quadratic elements",N))
% if N == 2
% exportgraphics(gca,"PiecewiseQuadratic.gif","Append",false)
% end
% for i = 1:10
% exportgraphics(gca,"PiecewiseQuadratic.gif","Append",true)
% end
end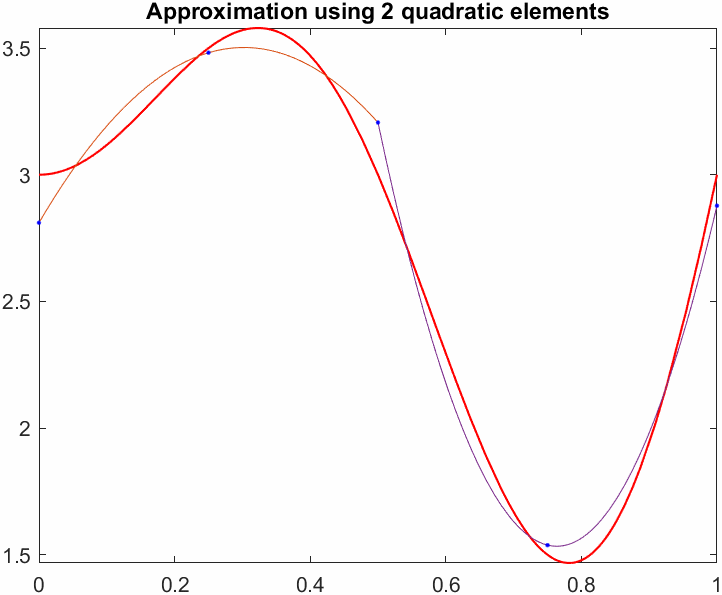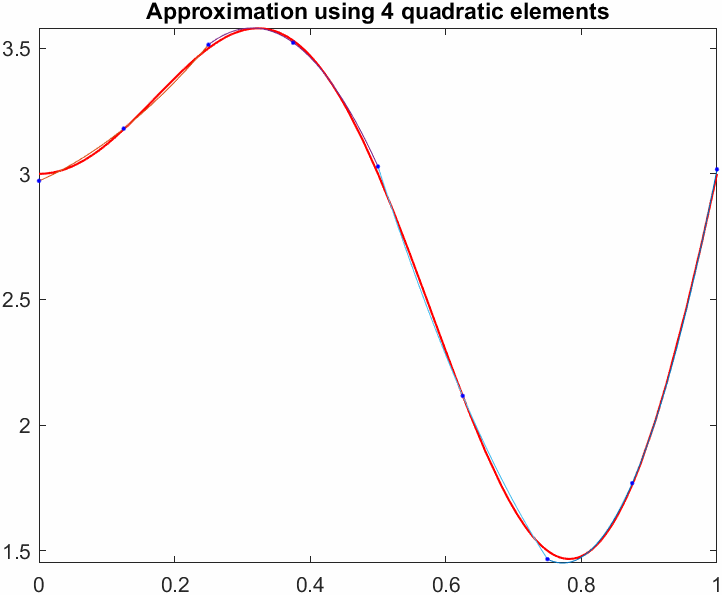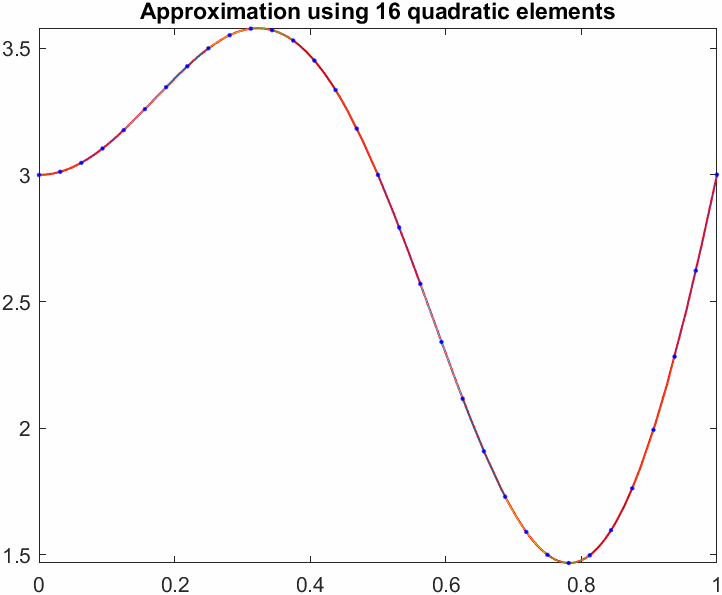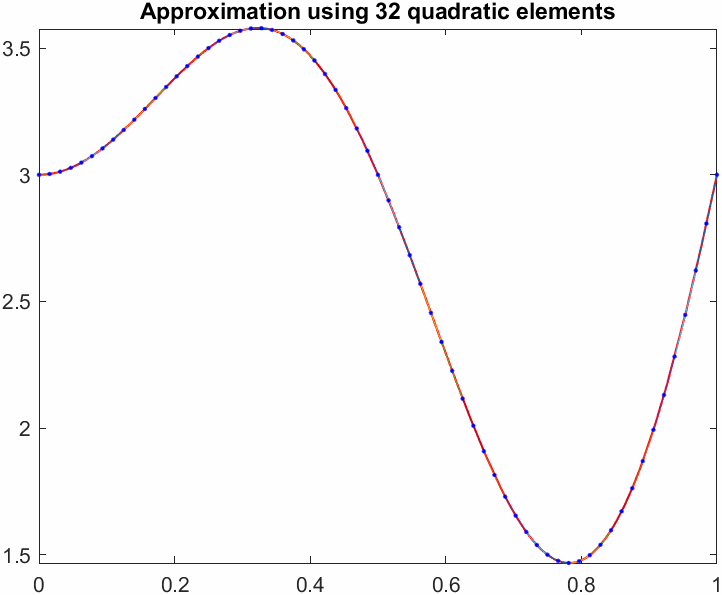
figure; hold on
plot(NN,L2Err,'-ko','DisplayName','Linear')
plot(NN,L2Err2,'-ks','DisplayName','Quadratic')
set(gca,'xscale','log','yscale','log')
xlabel("N"); ylabel("L_2 error")
xticks(NN)
xticklabels({'2','4','8','16','32'})
grid on
legend show
Note how the quadratic approximation not only has a lower initial error but also a steeper slope, meaning it converges faster.
figure; hold on
plot(NN,Time,'-ko','DisplayName','Linear')
plot(NN,Time2,'-ks','DisplayName','Quadratic')
set(gca,'xscale','log','yscale','log')
xlabel("N"); ylabel("Time (s)")
xticks(NN)
xticklabels({'2','4','8','16','32'})
yticks([0.5,1,2,4,8,16])
grid on
legend("show",location="northwest")