Table of contents
Interpolating from nodal values. Give som field in the nodal values of an element we can compute values somewhere inside the element using the basis functions as an interpolant. This section shows how to do this and how the choice of basis functions effect the interpolation accuracy.
Given some element in 2D
P = [0 0
1.0 0
0.9 1.0
-0.1, 1.2];We have some discrete scalar field in the nodes given by
U = [20
30
40
25];We can visualize this by
figure
patch("Faces",[1,2,3,4],'Vertices', P, 'CData', U, 'FaceColor', 'interp')
hold on; axis equal tight; colormap jet; colorbar
plot(P(:,1), P(:,2),'ok','MarkerFaceColor','k')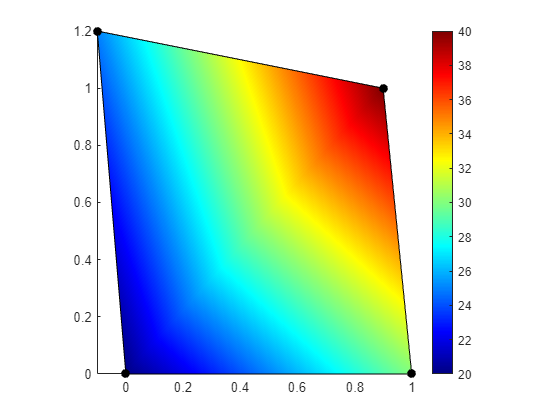
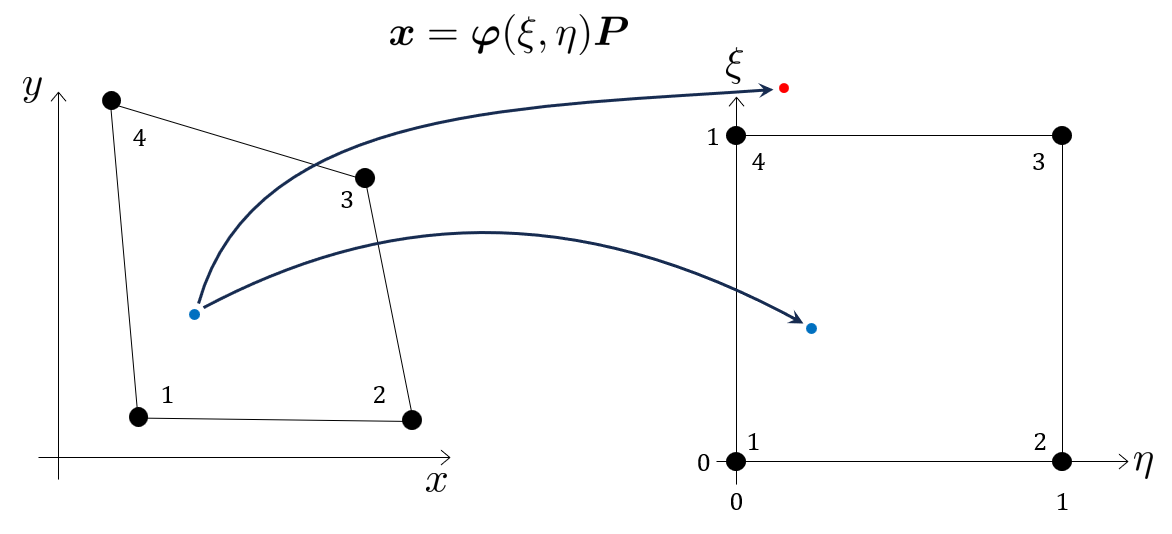
Now we want to know what the value is in the point .
We can use the basis functions for a four-noded quadliteral element to interpolate the nodal values. See how to derive basis functions or just grab the pre-computed basis functions. We have, for the element above, the basis functions defined for the parametric coordinates
phi = @(xi,eta)[(eta-1.0).*(xi-1.0),-xi.*(eta-1.0),eta.*xi,-eta.*(xi-1.0)];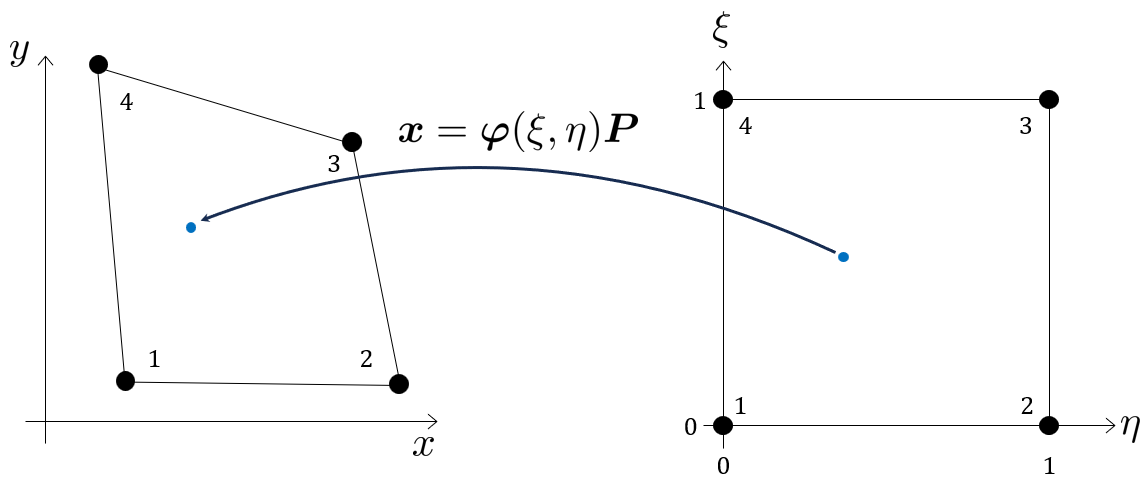
Now, we can easily interpolate using parametric coordinates by
syms xi eta
Uh = phi(xi, eta)*U;
Uh = simplify(Uh)E.g., in the midpoint we have
double(subs(Uh,[xi,eta],[0.5,0.5]))ans = 28.7500The issue is when we actually want the values as functions of the coordinates , i.e., , we need to solve a system of equations which, depending on the geometry of the element (the coordinates ), will be either linear or non-linear. For instance when is affine:
P = [0 0
2.0 0
2.0 1.0
0, 1];figure
patch("Faces",[1,2,3,4],'Vertices', P, 'FaceColor', 'w')
hold on; axis equal tight;
plot(P(:,1), P(:,2),'ok','MarkerFaceColor','k')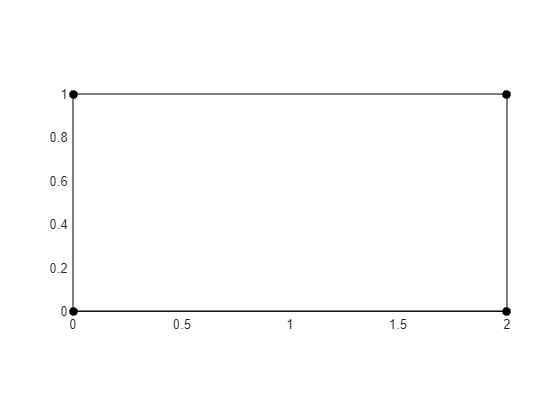
We want to solve for and
syms x y
eqs = phi(xi, eta)*P == [x y];
eqs = simplify(eqs)we see that this is trivial
[xi, eta] = solve(eqs,[xi,eta])we can then substitute this into to get
simplify(phi(xi,eta))which we can use as an interpolant to get
If, however, the element is not affine, e.g.,
P = [0 0
1.0 0
0.9 1.0
-0.1, 1.2];figure
patch("Faces",[1,2,3,4],'Vertices', P, 'FaceColor', 'w')
hold on; axis equal tight;
plot(P(:,1), P(:,2),'ok','MarkerFaceColor','k')
using and solving again for and we get the non-linear system of equations
syms x y xi eta
eqs = phi(xi, eta)*P == [x y];
eqs = simplify(eqs).'notice how we can not formulate a system of the form . We can, however, solve this equation system symbolically to get two solutions
[xi, eta] = solve(eqs,[xi,eta])xi =
eta =
here, in the two solutions and , only one is within the valid parametric space , which is and (after testing).
We can substitue the to get which we can evaluate in all nodes, we should get the identiy matrix.
xi = xi(1); eta = eta(1);
phi_xy = matlabFunction(simplify(phi(xi,eta)))phi_xy =
@(x,y)[x.*(-5.1e+1./2.0)-y.*5.0-sqrt(x.*-1.2e+1-y.*2.0+x.^2+3.6e+1).*(4.9e+1./2.0)+1.48e+2,x.*(6.1e+1./2.0)+y.*5.0+sqrt(x.*-1.2e+1-y.*2.0+x.^2+3.6e+1).*(5.9e+1./2.0)-1.77e+2,x.*-3.0e+1-y.*5.0-sqrt(x.*-1.2e+1-y.*2.0+x.^2+3.6e+1).*3.0e+1+1.8e+2,x.*2.5e+1+y.*5.0+sqrt(x.*-1.2e+1-y.*2.0+x.^2+3.6e+1).*2.5e+1-1.5e+2]phi_xy(P(:,1),P(:,2))ans = 4x4
1.0000 0 0 0
0 1.0000 0 0
0.0000 0 1.0000 0
0 0 0 1.0000Seems good! But note that, obviously, it is not efficient to have to deal with solving a non-linear system. Which is why we prefer to work in the parametric space if we can!
For our problem where we want to generate the function , we can now use
syms x y
Uh(x,y) = phi_xy(x,y)*UUh(0,0) = 20Now to visualize the interpolated field, it is again much easier to to do in the parametric space, i.e.,
N = 100;
xi = linspace(0,1,N);
eta = xi;
[Xi, Eta] = meshgrid(xi,eta);
UH = phi(Xi(:),Eta(:))*U;
PP = phi(Xi(:),Eta(:))*P;
X = reshape(PP(:,1),N,N);
Y = reshape(PP(:,2),N,N);
UH = reshape(UH,N,N);
figure; axis equal tight; hold on
surf(X,Y,Y*0,UH,'EdgeColor','none')
colormap jet; colorbar
contour(X,Y,UH,5,'EdgeColor','k')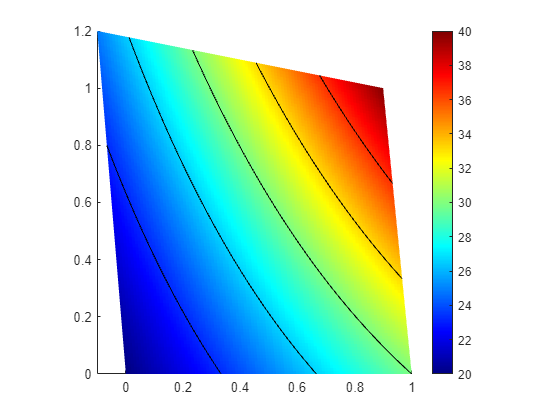
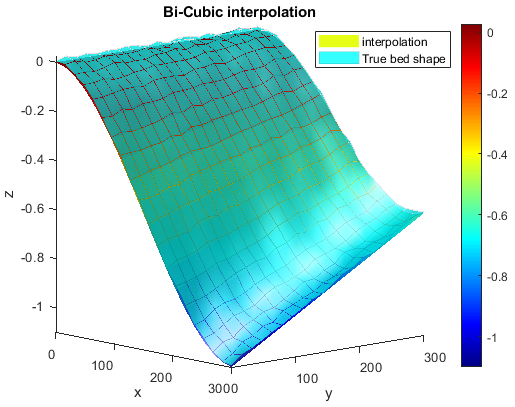
Here we can clearly see the curved (non-linear) nature of the bi-linear interpolant.