Download this page as a Matlab LiveScript
Table of contents
Compute for the quadrilateral element given by the coordinates below, use Gaussian quadrature to integrate!
P = [0 0
1 0
0.5 0.6
0 1];Solution:
figure
patch(P(:,1),P(:,2),'w','FaceColor','w'); hold on
plot(P(:,1),P(:,2),'ok','MarkerFaceColor','k','MarkerSize',8,'DisplayName','Nodes')
xlabel('x')
ylabel('y')
np = size(P,1);
xm = mean(P,1);
Tp = P+(xm-P)*0.2;
text(Tp(:,1),Tp(:,2),cellstr(num2str((1:np)')),'FontSize',14)
Using simple polygon area computation we can compute the area of this polygon.
area_geom = polyarea(P(:,1),P(:,2))area_geom = 0.5500The area (of any element) is given by the determinant of the Jacobian of the element integrated over the reference element.
We need the Jacobian
using the basis functions for the bi-linear element
phi_n = @(xi,eta)[(eta-1.0).*(xi-1.0),-xi.*(eta-1.0),eta.*xi,-eta.*(xi-1.0)];syms xi eta
phi(xi,eta) = sym(phi_n)The derivatives of the basis functions.
Bhat = [diff(phi,xi)
diff(phi,eta)]J = Bhat*PdetJ = det(J)area = int( int( detJ ,eta,0,1),xi,0,1 )vpa(area)Ok, above we used symbolic integration, but we need to use Gauss quadrature to integrate , we can see that the function is linear in and so one-point Gauss is sufficient to integrate it exactly!
Recall
where the points are given in the Gauss quadrature table and is the size (area) of the reference element.
we will use and with
xi = 1/2; eta = 1/2; w = 1;
area = vpa(subs(detJ))The strength of the Gaussian quadrature really shines when it comes to computing the area of curved elements. Remember, Gauss quadrature integrates these elements exactly!
Compute the area of this second order triangle with the nodal coordinates in
P = [0, 0.1
1 0
0 1
0.5 -0.1
0.5 0.6
-0.1 0.5]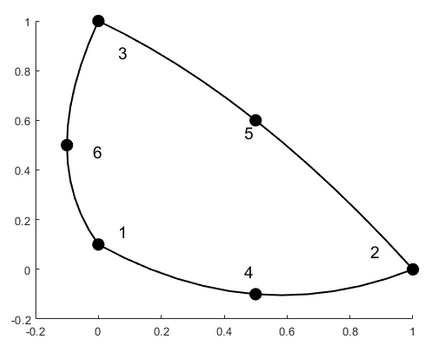
phi_n = @(xi,eta)[eta.*-3.0-xi.*3.0+eta.^2.*2.0+xi.^2.*2.0+eta.^2.*xi.^2.*1.6e1+1.0,xi.*(xi.*2.0-1.0),eta.*(eta.*2.0-1.0),xi.*(xi+eta.^2.*xi.*4.0-1.0).*-4.0,eta.^2.*xi.^2.*1.6e1,eta.*(eta+eta.*xi.^2.*4.0-1.0).*-4.0];phi = sym(phi_n);syms xi eta
Bhat = [diff(phi,xi)
diff(phi,eta)];J = Bhat*P;detJ = det(J)Now we compute the integral of the above expression using a second order Gauss rule since the highest polynomial term is 3.
gp = [0.5, 0
0.5, 0.5
0, 0.5];
gw = 1/3*[1;1;1];The area of the reference triangle is , then we use the sum:
dk_hat = 1/2;
I = 0;
for i = 1:3
xi = gp(i,1);
eta = gp(i,2);
w = gw(i);
I = I + subs(detJ)*w*dk_hat
endvpa(I)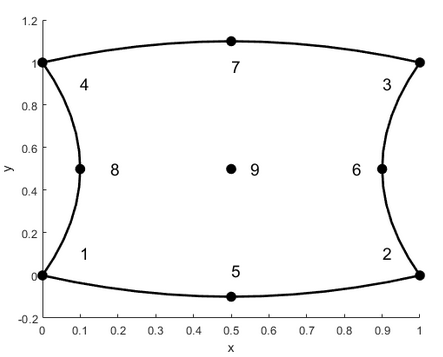
with nodes in
P = [0 0
1 0
1 1
0 1
0.5 -0.1
0.9 0.5
0.5 1.1
0.1 0.5
0.5 0.5];Use Gaussian quadrature rules to integrate the area.
Use the code below to get the Gauss points and weights for the quadrilateral element:
order = 2; %Select the Gauss order here
[GP,GW] = GaussQuadrilateral(order);We see that the area is supposed to be 1 due to symmetry.
phi = @(xi,eta)[(eta.*-3.0+eta.^2.*2.0+1.0).*(xi.*-3.0+xi.^2.*2.0+1.0),xi.*(xi.*2.0-1.0).*(eta.*-3.0+eta.^2.*2.0+1.0),eta.*xi.*(eta.*2.0-1.0).*(xi.*2.0-1.0),eta.*(eta.*2.0-1.0).*(xi.*-3.0+xi.^2.*2.0+1.0),xi.*(xi-1.0).*(eta.*-3.0+eta.^2.*2.0+1.0).*-4.0,eta.*xi.*(xi.*2.0-1.0).*(eta-1.0).*-4.0,eta.*xi.*(eta.*2.0-1.0).*(xi-1.0).*-4.0,eta.*(eta-1.0).*(xi.*-3.0+xi.^2.*2.0+1.0).*-4.0,eta.*xi.*(eta-1.0).*(xi-1.0).*1.6e1];
phi = sym(phi);
syms xi eta
Bhat = [diff(phi,xi)
diff(phi,eta)];
J = Bhat*P;
detJ = det(J)Here we evaluate the expression numerically:
detJ = matlabFunction(detJ)detJ =
@(eta,xi)eta.*(-3.6e+1./2.5e+1)+xi.*(4.0./2.5e+1)+eta.*xi.*(4.8e+1./2.5e+1)-eta.*xi.^2.*(4.8e+1./2.5e+1)-eta.^2.*xi.*(4.8e+1./2.5e+1)+eta.^2.*(3.6e+1./2.5e+1)-xi.^2.*(4.0./2.5e+1)+eta.^2.*xi.^2.*(4.8e+1./2.5e+1)+2.9e+1./2.5e+1area = detJ(GP(:,2),GP(:,1)).'*GWarea = 1.0000function [GP,GW] = GaussQuadrilateral(order)
%GaussQuadrilateral Gauss integration scheme for quadrilateral 2D element
% [x,y] in [0,1]
[gp,gw] = gauss(order,0,1);
[GPx,GPy] = meshgrid(gp,gp);
[Gw1,Gw2] = meshgrid(gw,gw);
GW = [Gw1(:), Gw2(:)];
GW = prod(GW,2);
GP = [GPx(:), GPy(:)];
end
function [x, w, A] = gauss(n, a, b)
%------------------------------------------------------------------------------
% gauss.m
%------------------------------------------------------------------------------
%
% Purpose:
%
% Generates abscissas and weights on I = [ a, b ] (for Gaussian quadrature).
%
%
% Syntax:
%
% [x, w, A] = gauss(n, a, b);
%
%
% Input:
%
% n integer Number of quadrature points.
% a real Left endpoint of interval.
% b real Right endpoint of interval.
%
%
% Output:
%
% x real Quadrature points.
% w real Weigths.
% A real Area of domain.
%------------------------------------------------------------------------------
% 3-term recurrence coefficients:
n = 1:(n - 1);
beta = 1 ./ sqrt(4 - 1 ./ (n .* n));
% Jacobi matrix:
J = diag(beta, 1) + diag(beta, -1);
% Eigenvalue decomposition:
%
% e-values are used for abscissas, whereas e-vectors determine weights.
%
[V, D] = eig(J);
x = diag(D);
% Size of domain:
A = b - a;
% Change of interval:
%
% Initally we have I0 = [ -1, 1 ]; now one gets I = [ a, b ] instead.
%
% The abscissas are Legendre points.
%
if ~(a == -1 && b == 1)
x = 0.5 * A * x + 0.5 * (b + a);
end
% Weigths:
w = V(1, :) .* V(1, :);
end